
|

1. Les grandes formes.
1.1. Antécédent.
Selon Sandra Aube, l’état actuel du tympan relève d’une "reconstitution des années 1980". Une photo de Robert Byron montre la situation dans les années 1930 :
http://archnet.org/print/preview/mediacontents=40098
(consulté en mai 2019)

Deux remarques à propos de ce document où on discerne les grandes lignes de la composition :
- l’étoile centrale est entièrement entourée par un ruban. Aujourd’hui ce n’est plus le cas. C’est probablement un choix esthétique permettant une étoile centrale plus grande.
- il semble que le ruban entre les formes polygonales est moins large que l’actuel (c’est assez visible au niveau des polygones en forme d’ailes de papillon).
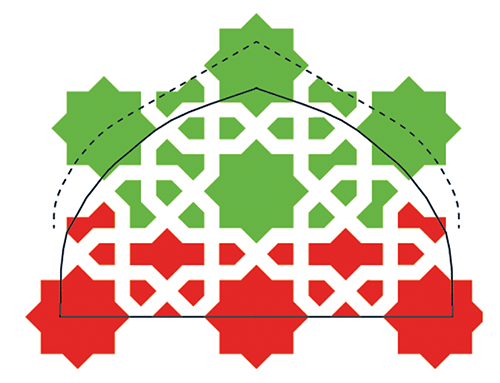
En vert la situation ancienne, avec en plus foncé les pièces qui disparaîtront dans la nouvelle version, obtenue par ajout des pièces oranges.
La photo ne dit rien sur le détail du motif de la décoration. À notre connaissance, on ne trouve le motif actuel sur aucun monument ancien, et nous penchons plutôt pour une création récente.
Par ailleurs, la composition initiale ne relevait peut-être pas de la technique de continuité du décor entre intérieur et extérieur des polygones. Le ruban initial semblant moins large, on trouvait peut-être quelque chose dans le style de ce tympan ouzbek :


1.2. La configuration actuelle.
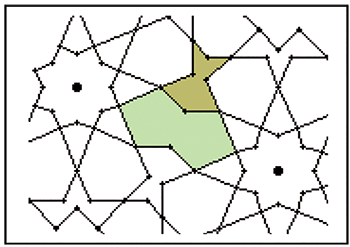
L’ensemble du tympan (hors écritures) présentant à peu près une symétrie par rapport à l’axe vertical médian, on limitera les dessins à la moitié droite.
Ce schéma a été établi par l’observation du détail de la décoration.
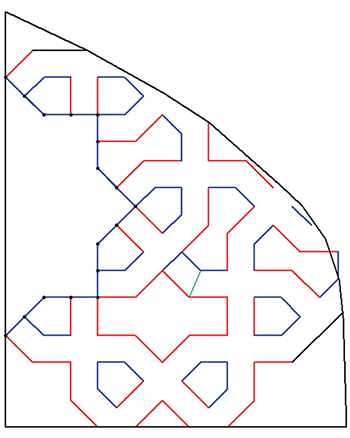
Les grandes formes polygonales n’utilisent que deux longueurs L1 et L2 telles que = 2
Le ruban entre les polygones utilise en plus une longueur L3 telle que = (2(2- 2))
2 est la longueur de diagonale d’un carré de côté 1. L’ensemble relève de la géométrie du carré.
D’ailleurs, il est possible de reconstituer la structure entière à partir d’un unique module carré de base.
2. Le détail de la décoration.
2.1. Les règles respectées
Ce sont les règles habituelles que l’on rencontre dans ce type de panneau :
- une étoile à chaque sommet des grands polygones
- une symétrie axiale locale par rapport à chacun des côtés des polygones
- une parfaite continuité du motif entre l’intérieur et l’extérieur des polygones. Sans les changements de couleur qui permettent de visualiser les grandes formes polygonales, l’œil ne verrait qu’un tapis continu régulier.
2.2. Les groupes de base
Une partie importante de la décoration est constituée par la répétition de deux motifs de base :
- l’un (ronds rouges) est formé par une étoile à 8 pétales
- l’autre (carrés verts) est moins directement perceptible.
2.3. Construction détaillée des deux motifs de base.

Traces
Deux carrés de même taille, de même centre, et décalés de 45° forment une étoile régulière à 8 pointes.
On prolonge les côtés de cette étoile pour en obtenir une deuxième.

Explication
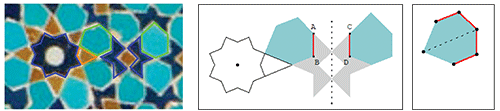
À gauche : nous faisons l’hypothèse que les deux formes entourées en vert sont identiques, mais dans des positions différentes.
Au milieu : la symétrie des deux pièces grises par rapport à l’axe en pointillés implique que AB = CD.
À droite : il s’ensuit que les pétales (qui ont leur propre axe de symétrie) ont 4 côtés de même longueur.
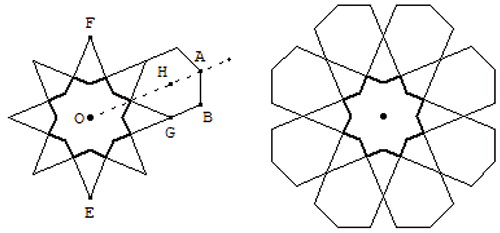
Traces
La parallèle à (EF) passant par G
coupe l’axe pointillé en H.
Puis on construit le losange GHAB.
Puis par symétrie le premier pétale.
Puis les autres.
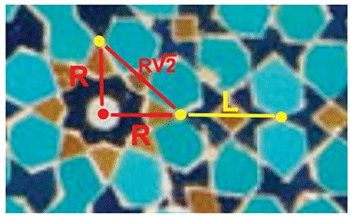
Explication
Pythagore dans un des deux triangles rectangles donne :
(2R+L)² + (2R+L)² = (2R+2L)²
4R² + 4RL + L² + 4R² + 4RL + L² = 4R² + 8RL + 4L²
4R² = 2L²
2R² = L² donc L = R 2
Or R 2 est aussi la longueur de diagonale du carré de côté R :

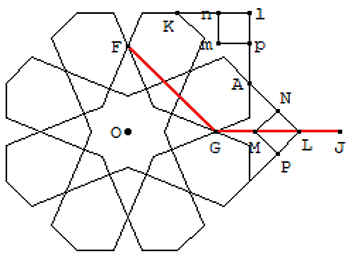
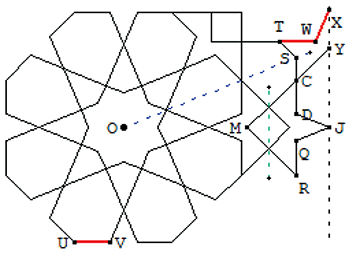
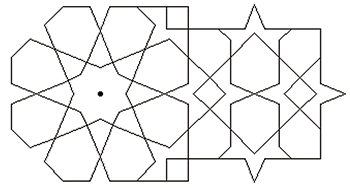
Traces
Construire J par rotation de F autour de G de 135°.
(KA) coupe (OJ) en L.
Construire M tel que GM = JL.
Construire le carré de diagonale ML.
Par rotation de 45° autour de O, construire les points mnlp.
Construire CDQR par symétrie par rapport au pointillé vert.
La droite (RC) coupe le pointillé bleu en S.
T est le symétrique de C par rapport au pointillé bleu.
W est tel que TW = UV de même direction.
X s’obtient par rotation de T autour de W de 135°.
(MC) et (JX) se coupent en Y.
Terminer par symétries axiales.
bilan numérique
La construction présente 6 longueurs différentes :
L1 L2 L3 L4 L5 L6
Elles sont toutes reliées entre elles, par exemple de la façon suivante :
= 1+ 2 = (2+ 2) = (2+ 2) - 1
= (1+ ) = 1+ 1/ 2
ce qui confirme bien le rôle fondamental joué par le nombre 2 .
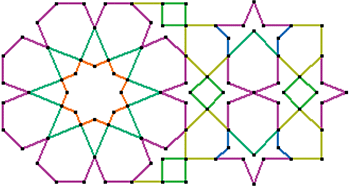
Remarque
Le chevauchement partiel de deux étoiles induit la création de deux pièces supplémentaires.

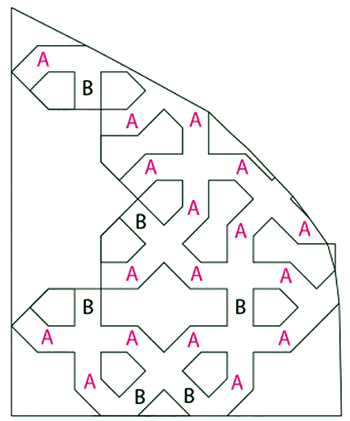
2.4. Les problèmes.
Les deux motifs de base vus précédemment ne suffisent pas à rendre compte de la totalité du dessin. Deux types de configuration, notés A et B, conduisent à une situation problématique.
(nous ne parlerons pas des irrégularités ponctuelles et mineures situées par exemple sur le pourtour du tympan ou concernant les couleurs).
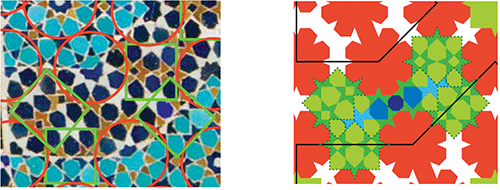
Problème A
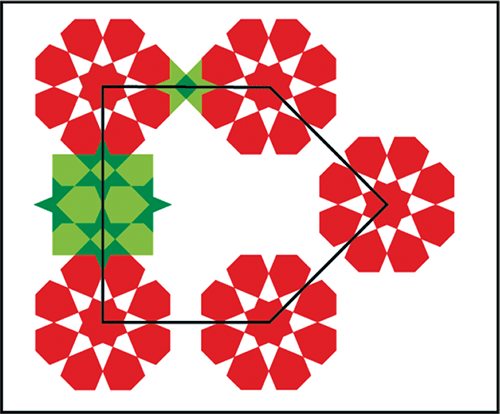
À gauche : repérage des deux motifs de base, avec chevauchement partiel de deux carrés verts.
À droite : les étoiles rouges et les parties de carrés (pointillés vert foncé) sont conformes aux motifs de base. Les pièces vertes hors pointillés font encore partie du même répertoire. Mais pour terminer le dessin, l’artiste a du créer 3 nouvelles pièces : en bleu foncé un octogone régulier, en bleu moyen un hexagone, et en bleu clair une sorte de papillon, les deux dernières pièces ayant un (unique) axe de symétrie.
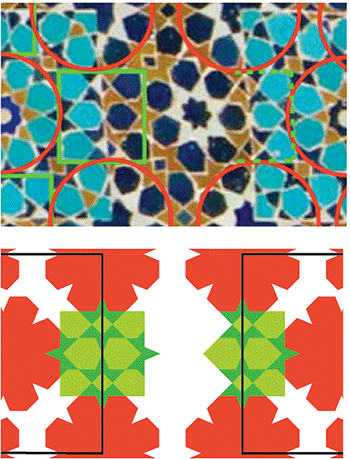
Problème B
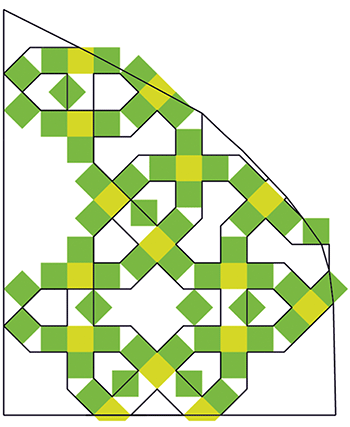
L’artiste a commencé par positionner un carré vert complet à gauche et un partiel à droite.
Ensuite, entre les deux, il a placé des parties de carrés (indiquées par les pointillés jaunes)
Puis (page suivante), il a encore ajouté deux pièces.
Toutes les pièces vertes appartiennent bien au répertoire des deux motifs de base.
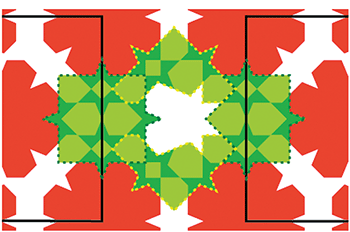
L’espace restant ne peut pas être complété avec les pièces habituelles. L’artiste n’a pas voulu en faire une nouvelle pièce (peut-être parce que sa taille la rendrait trop voyante).
Il a préféré transformer cet espace en une étoile à 7 pointes. Mais pour cela il a du déformer les pièces avoisinantes pour en faire 7 pétales pas trop irréguliers. Visuellement, il s’en sort plutôt bien, les arrangements sont assez discrets. Malheureusement, on perd en précision mais surtout on sort de la famille mathématique basée sur le nombre 2, qui régissait jusque là très élégamment la totalité du dessin.

2.5. Des solutions.
Proposition 1.
Concernant le problème de type B, l’environnement de la zone embarassante incite tout naturellement à ajouter une quatrième étoile contre le carré vert de gauche. L’agencement est parfaitement conforme.
L’inconvénient est que l’on enfreint la deuxième règle énoncée page 3, car on a perdu la symétrie locale par rapport à l’axe (AB).
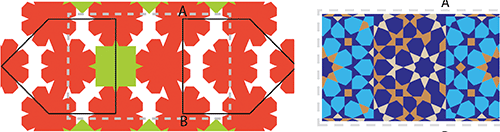
Il nous a semblé que cette entorse était moins grave que celle de l’étoile à 7 pointes, et c’est cette option que nous avons choisie pour la reconstitution du tympan de la planche1.
Planche 1 : le dessin utilise les 7+2 (chevauchement partiel d’étoiles) pièces normales du motif de base, augmentées des 3 pièces liées au problème A, qui reste inchangé. Plus perte de symétrie locale sur un côté du pentagone.
Proposition 2.
Autre piste possible, on peut décider de garder intacte la structure générale du tympan avec ses grandes formes polygonales, mais de diminuer la taille des petites pièces du motif. Pour assurer la compatibilité du nouveau motif avec la structure générale, on a diminué le motif initial d’un coefficient ?2.
Ce changement a permis de respecter strictement les règles de la page 3,

mais il a fallu quand même créer trois petites pièces supplémentaires
(qui sont de la même famille 2 ) :
Planche 2 : le dessin utilise les 7+2 pièces normales du motif de base, plus 3 pièces supplémentaires.
Les problèmes A et B sont résolus. Pour une raison esthétique, nous avons redonné aux pétales qui se chevauchent la même forme qu’aux autres pétales.
Proposition 3.
On peut aussi, sans modifier la structure générale des grandes formes, changer le motif décoratif.
Le motif utilisé doit bien entendu rester dans la famille de la géométrie du carré, basée sur le nombre 2.

Celui présenté ici est en partie inspiré par la planche 59 du livre de Jules Bourgoin : "Les éléments de l’art arabe : le trait des entrelacs " (consultable sur Gallica).
Ce motif utilise un jeu de 7 pièces, qui toutes peuvent s’obtenir très facilement à partir de la même étoile à 8 pointes :
Planche 3 : le dessin utilise le même nombre de pièces que le motif original (7 de base + 2 en cas de chevauchement de deux étoiles). Les problèmes A et B ont disparu. Le motif respecte toutes les règles énoncées page 3.
Visuellement l’ensemble est assez proche du tympan de Yazd.
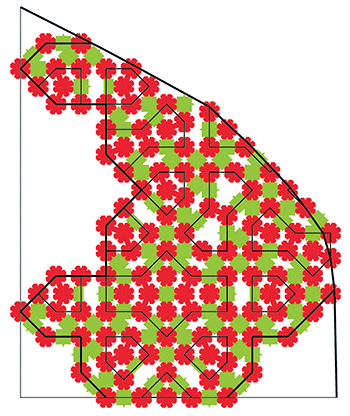
Planche 4 : une proposition de tympan complet, avec remplissage des grandes étoiles en continuité.
3. Variante.
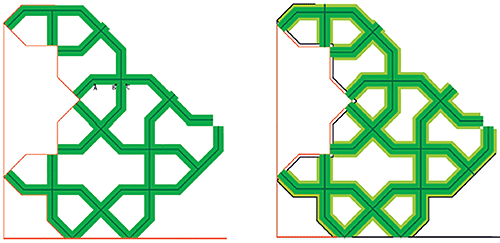
À gauche : reprise de la structure générale présentée page 2, en faisant ressortir l’espace entre les grandes formes polygonales (le "ruban"), et on ajoutant en son "milieu" le trait vert foncé appelé l’armature du dessin.
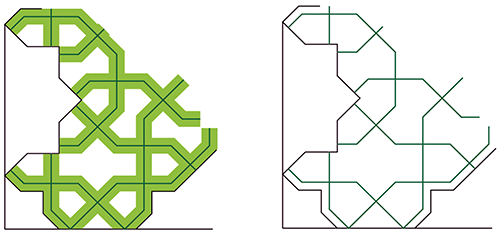
À droite : l’armature seule. Maintenant on inverse le point de vue en considérant
qu’on peut obtenir le dessin de gauche à partir de celui de droite en élargissant
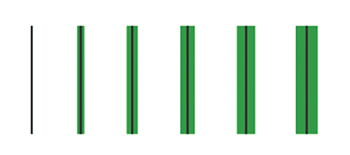
symétriquement la largeur du trait de l’armature.
Voir une petite animation sur youtube : https://youtu.be/Piu_RRbQXBM
Quand on modifie la largeur du trait, les pentagones et le triangle changent de taille, mais ne changent pas de forme. Par contre, les autres polygones changent de taille mais aussi de forme. On s’en rend très bien compte sur l’animation. Tout bouge, mais pas de la même façon ! La difficulté est de trouver une nouvelle largeur de trait qui reste compatible avec le détail du motif décoratif, c’est-à-dire qui préserve les règles énoncées page 3.
Une condition nécessaire (mais pas suffisante !) est de veiller à rester dans la famille géométrique du nombre 2.
Pour plus d’explications, nous nous permettons de renvoyer à notre site : http://patterns-islamiques.fr
qui traite la même question pour la famille géométrique du nombre 5 .
À gauche : la solution retenue, dans laquelle BC mesure la moitié de AB ; dans le cas du tympan de Yazd, ces deux longueurs étaient égales.
À droite : on a superposé les deux structures, l’armature est bien la même pour les deux.
Planches 5 et 6 : reprise des deux motifs avec un ruban moins large.







