|

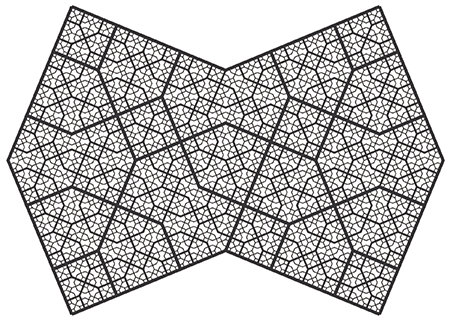
Les grandes formes.
1.1. Analyse.
La construction présente 5 longueurs différentes
L1 L2 L3 L4 L5
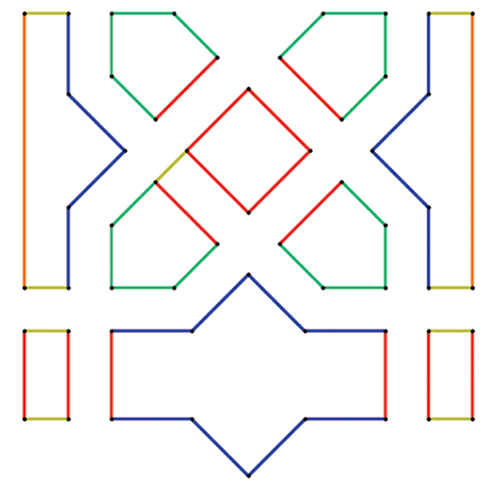
Elles sont toutes reliées entre elles, par exemple de la façon suivante :
L1/L2 = √2 L1/L4 = 2 L3/L1 = √2 - 1/2 L5/L3 = √2+ 2

Tous les autres rapports possibles peuvent se déduire des précédents. Nous sommes bien dans la famille géométrique du carré, caractérisée par le nombre √2 .
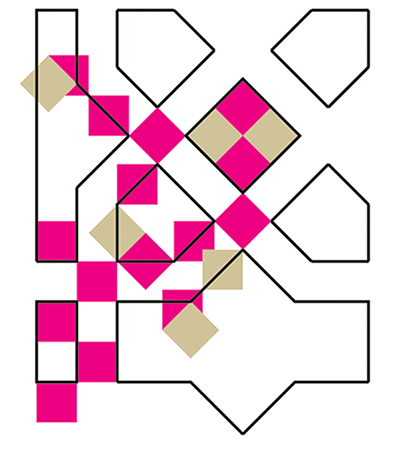
D’ailleurs un unique module carré (le quart du carré central) permet de retrouver facilement toutes les grandes formes.
Parmi celles-ci, la forme pentagonale à 3 angles droits et 4 côtés égaux jouera un rôle central dans cette étude.
1.2. Le ruban.
La méthode par écartement des pièces ne fonctionne pas ici, parce que les longueurs AB et CD ne sont pas égales.
Il faut employer la méthode par grossissement des traits, déjà présentée dans un article précédent sur le tympan de Yazd.
En vert foncé l’armature, à partir de laquelle se fait l’élargissement. Voir une petite animation sur youtube :
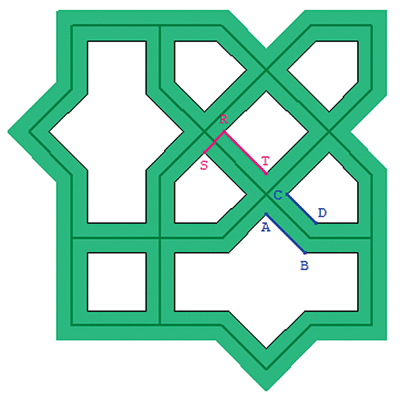
La largeur relative du ruban est définie par "largeur réelle du ruban" divisée par "longueur réelle du côté du carré central". À Mechhed elle vaut 0,5 ; c’est-à-dire que RS est la moitié de RT (évident en regardant la décoration du ruban).
On voit très bien sur l’animation que, lorsque le trait grossit, les carrés et les pentagones changent de taille, mais ne changent pas de forme. Par contre le polygone à 10 côtés de déforme continument.
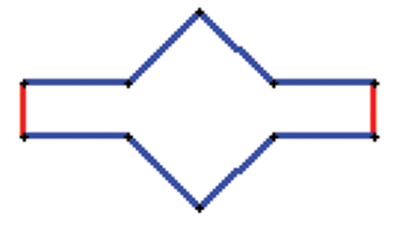
Mais d’une façon particulière : quelle que soit la largeur du ruban, ce polygone aura
toujours 8 côtés égaux et les 2 derniers de même longueur que le côté du carré central.
1.3. L’armature.
Elle peut être obtenue de la façon suivante :

1- quatre étoiles régulières à huit pointes engendrent une croix qu’on peut décomposer en un carré central et quatre pentagones. Ces pentagones ont par construction la particularité de présenter 3 angles droits et 4 côtés de même longueur
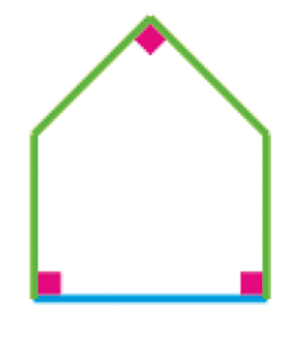
2- cette croix, par duplications, peut générer un pavage
3- formation des polygones à 10 côtés
4- l’armature qui sert de base à l’élargissement du trait

La décoration.
2.1. Inventaire.
Les pièces "bizarres"
1 : utilisation dans les rubans latéraux d’une pièce qui n’apparaît pas ailleurs, alors que l’on pouvait occuper le même espace avec les pièces déjà existantes. Peut-être la volonté de souligner visuellement un axe de symétrie ?
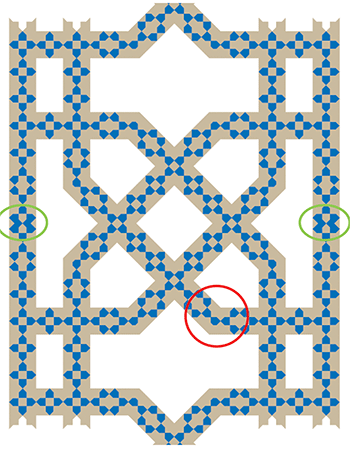
2 : présence, sur chaque coude à 135°, d’une pièce formée par la superposition partielle de deux étoiles (ce qui de plus a obligé à créer une nouvelle pièce "cheville").
Nous n’avons trouvé aucun autre exemple de cette particularité sur d’autres monuments.
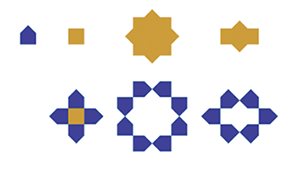
Les 4 pièces "régulières"
1 et 2 : on retrouve le pentagone particulier et le carré, les mêmes qu’au paragraphe 1.1., à une taille réduite. Le coefficient de réduction est de 4+2 (environ 6,83). On peut fabriquer le carré à partir du pentagone.
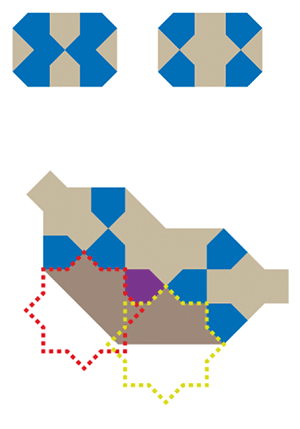
3 : l’étoile régulière à 8 pointes, qu’on peut fabriquer à partir du pentagone.
4 : le polygone à 10 côtés qui n’est pas une réduction de celui du paragraphe 1.1. (on a vu que la présence du ruban change la forme de ce polygone), et qu’on peut aussi fabriquer à partir du pentagone.
Ce pentagone permet donc à lui seul d’engendrer toutes les autres pièces.
2.2. Prolongement par continuité.

Rappelons les trois règles habituelles dans ce type de composition :
- une étoile à chaque sommet de grand polygone
- une symétrie axiale locale par rapport à chacun des côtés de ces polygones
- une parfaite continuité du motif entre l’intérieur et l’extérieur des polygones
Dans le cas présent la première règle n’est pas satisfaite, du fait de la particularité précisée au point 2 dans le paragraphe précédent.
Nous allons maintenant présenter des solutions pour réaliser, à partir de la même structure géométrique des grandes formes, une composition qui respecte ces trois règles.
Il est possible de remplir les grandes formes polygonales en continuité avec le détail du motif du ruban, moyennant une petite modification du ruban latéral.
Réduire la taille du motif.
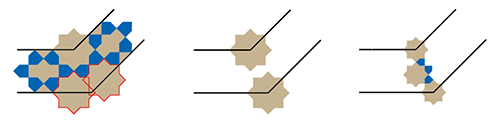

Pour passer le coude à 135°, on doit réduire la taille de l’étoile.
La réduction minimale est indiquée ci-contre, c’est celle que nous avons utilisée pour élaborer ce panneau (où les 3 règles sont respectées) :
Utiliser un autre motif décoratif.
Modifier la largeur du ruban.

On peut essayer de donner un peu de souplesse en élargissant le ruban. Comme expliqué au paragraphe 1.2., il faut utiliser la méthode par grossissement des traits, qui modifie la forme du polygone à 10 côtés. Le dessin obtenu est certes très ressemblant, mais il n’est pas strictement conforme à l’original.
Voici tout de même une version avec une largeur relative du ruban de (environ 0,71). Dans cette version le polygone à 10 côtés a tous ses côtés de même longueur, ce qui n’est pas le cas dans la version de Mechhed :

Contrefaçon !
Cette planche ressemble beaucoup à la précédente, car la largeur relative du ruban y est encore de .

La différence vient du polygone à 10 côtés. Il possède bien 8 côtés de même longueur, mais les deux côtés restants n’ont pas la même longueur que le côté du carré central. Or nous avons vu au paragraphe 1.2. que c’est une condition de conformité au modèle original. C’est le choix du motif décoratif qui a conduit à cette situation. Bien sûr, cela n’empêcherait pas d’en faire une frise comme à Mechhed, mais cela pourrait poser des difficultés pour d’autres compositions.
Une curiosité.

Libre interprétation d’un motif provenant probablement de l’Alhambra, Grenade, Espagne.

Motifs apparentés.
Nous présentons dans cette section quelques exemples de compositions dérivées du motif de Mechhed. La présence du pentagone particulier est un indice fort d’une filiation possible. On repère très facilement ses 3 angles droits et ses 4 côtés égaux, et cette pièce n’est pas déformée par la présence d’un ruban.
Ces compositions peuvent se déduire les unes des autres de multiples façons, nous ne faisons que proposer des pistes éventuelles.
3.1. Mosquée du Vendredi, Yazd, Iran.

Son tympan a fait l’objet d’un article précédent.
La largeur relative du ruban y est de (environ 0,71).
En partant de la version du motif de Mechhed qui a la même largeur de ruban (présentée en 2.5.), il est possible de retrouver la structure de ce tympan de la façon suivante (les pièces grises servent de repère pour le positionnement de pièces ultérieures) :
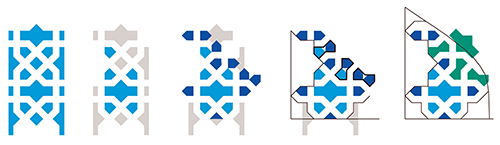
Remarque 2 : la pièce en forme de nœud papillon a un statut comparable à celui du polygone à 10 côtés. C’est-à-dire que sa forme dépend de la largeur du ruban. On le voit très bien sur l’animation proposée pour le tympan de Yazd : https://youtu.be/Piu_RRbQXBM
En l’absence de ruban la pièce a 8 côtés égaux, ce n’est plus vrai avec le ruban.

On rencontre souvent cette pièce en association avec le pentagone à 3 angles droits et 4 côtés égaux.
3.2. L’octogone régulier.
Ces trois documents présentent en leur partie centrale le même motif de décomposition d’un grand octogone

1 : madrasa Sher-Dor, Samarcande, Ouzbékistan
L’octogone est entouré de polygones à 10 côtés du même type que ceux de Mechhed
2 : mausolée d’I’timâd ud-Daulah, Agra, Inde
Le cercle de 8 étoiles rappelle celui de 4 étoiles du paragraphe 1.3.
3 : tombeau d’Akbar, Sikandra, Inde
L’octogone est tourné de 45°. On retrouvera ce style de motifs au paragraphe 3.5.
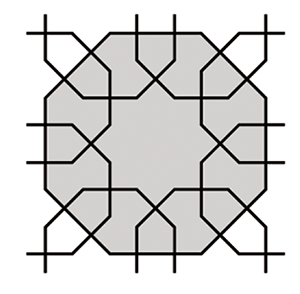
On peut obtenir cette décomposition de l’octogone à partir du pavage vu au paragraphe 1.3.
On peut aussi dire que plusieurs octogones identiques engendrent le motif du pavage.
Tout se tient …
Nous avons choisi la version de Samarcande, parce qu’on y retrouve les polygones à 10 côtés de Mechhed.
Par commodité on a repris la même largeur relative de ruban qu’à Yazd ; d’ailleurs il est facile de reconstituer tout le motif à partir du tympan de Yazd.
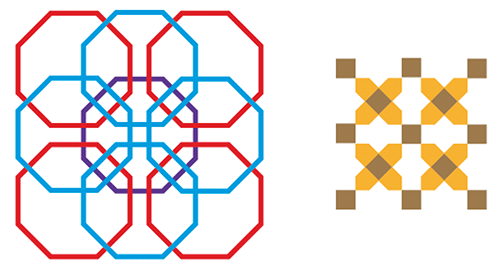


Ensemble architectural Khazrat-i-Imam, Tachkent, Ouzbékistan.
Vue partielle d’un tambour circulaire. Dans la partie encadrée sur la photo, les grandes formes peuvent être obtenues à partir du motif du paragraphe précédent de la façon suivante (on termine par des rotations successives de 90° autour de la petite croix rouge) :

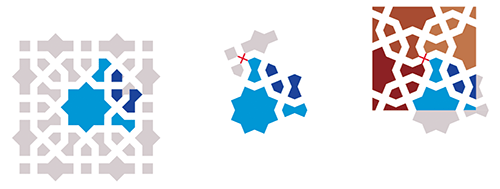
La frise du tambour peut ensuite être reconstituée à partir de cette cellule de base, en la transformant plusieurs fois par une succession de symétries axiales par rapport aux axes pointillés :
Remarquons au passage qu’il a fallu calculer précisément les dimensions du motif pour obtenir, sur la périphérie du tambour cylindrique, un nombre entier pair de cellules !
Encore un bel exemple où la décoration du monument a été obligatoirement conçue en lien très étroit avec son architecture.


Nous proposons page suivante une libre adaptation avec un autre motif décoratif (on a gardé la même largeur de ruban que dans l’exemple précédent).
Remarque : en modifiant légèrement le choix de la cellule de base, il est possible d’obtenir ce pavage périodique :


Musée des arts appliqués, Tachkent, Ouzbékistan.
Le motif est sculpté sur un poteau en bois cylindrique (d’où un raccord quelque peu raccourci le long du pointillé).


Ci-dessous une proposition de décoration. La forme en V inhabituelle s’apparente à celle qui apparaît furtivement sur les bordures extérieures à Mechhed (un peu déformée par la présence du ruban)

3.5. Mausolée de Mohammad Ghaus,
Gwalior, Inde.
On trouve sur ce site de nombreuses fenêtres jali en pierre ajourée.
Premier exemple :

Le motif est régulier et périodique (si on ne regarde pas trop les bords).
Il utilise un jeu de seulement 3 pièces, déjà rencontrées :
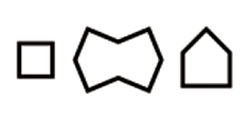
En fait, la partie en pierre constitue un ruban qui sépare des pièces vides apparaissant en creux. On a vu (paragraphe 3.1.) que le ruban déforme la pièce en nœud papillon, mais ça ne se voit quasiment pas si le ruban est mince.

Deuxième exemple :
Cette composition, fabriquée avec le même jeu de 3 pièces, présente à première vue un aspect très peu ordonné.

Pourtant elle a été précisément construite !
On peut mettre en évidence les formes cachées par grossissement de certains rubans. Cette méthode a été utilisée dans plusieurs monuments, par exemple
(photo ci-contre) au mausolée d’I’timâd ud-Daulah, Agra, Inde (avec un jeu de pièces un peu différent de celui de Gwalior).

Remarque : on retrouve, à l’intérieur des octogones, la décomposition vue au paragraphe 3.2.
Adaptation de la photo précédente avec le jeu de 3 pièces de Gwalior.
Peut-être existe-t-il une fenêtre de ce type sur le site indien !

Vers l’infini …
Le jeu de 3 pièces utilisé ( ) dans ces grilles présente les deux propriétés suivantes :
1- chacune des pièces, seule, peut engendrer un pavage périodique
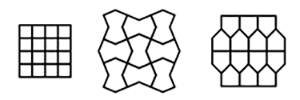
(infini "à l’horizontale")
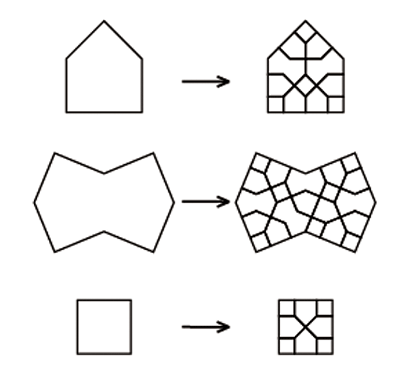
2- chacune des pièces peut être décomposée en utilisant le même jeu de 3 pièces à une échelle réduite, le coefficient de réduction étant de 2 +
(environ 3,41).
D’où, par itération du processus, la possibilité d’une mise en abyme potentiellement sans fin (infini "à la verticale").
Ci-dessous un exemple à quatre niveaux :