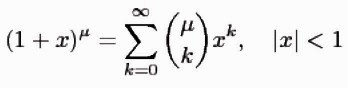|
Souvent connu en tant que poète pour ses fameux quatrains, Omar Khayyâm était également un éminent mathématicien. Ses efforts notamment dans la résolution des équations algébriques auraient influencé René Descartes au XVIIe siècle dans la fondation de la géométrie analytique. Il est intéressant de voir que ces deux hommes ont eu plus que les mathématiques en commun. Descartes, théologien et recteur de l’Université d’Utrecht, fut accusé d’athéisme. Khayyâm avant lui, avait également risqué la persécution pour sa liberté de pensée notamment dans le domaine religieux.
Mathématiquement, la méthode cartésienne se situe dans le prolongement de la méthode de Khayyâm. Descartes découvre que certains points d’intersection peuvent représenter des racines imaginaires et il donne ainsi une solution complète pour les réponses négatives, positives et imaginaires.
Plus que pour son important traité sur l’algèbre, Khayyâm était davantage connu en Orient comme l’astronome qui a réformé le calendrier solaire iranien. Ce ne fut qu’au XIXe siècle que ses recherches algébriques commencèrent à être étudiées et découvertes, et c’est pour cette raison que ses travaux n’ont pas eu l’impact qu’ils auraient dû avoir dans le monde scientifique. Quand ses recherches attirèrent l’attention des savants, principalement au XIXe siècle, les sciences avaient déjà atteint un niveau plus élevé, de sorte que la connaissance de l’œuvre du savant iranien revêtait seulement une importance historique. L’historien américain des sciences George Sarton écrivit pourtant à son propos : « Khayyâm est le premier à s’être intéressé aux équations linéaires, carrées et cubiques. Il a présenté une catégorisation admirable des équations dont il a cherché les formes géométriques. Son traité d’algèbre introduit une pensée bien ordonnée. Ce traité est l’un des plus remarquables du Moyen-âge. »
En réalité, Khayyâm a effectivement contribué aux sciences, en particulier en réalisant une suite de découvertes dans le domaine des mathématiques, de l’astronomie et de la physique. Pour la première fois de l’histoire des mathématiques, il a donné une classification complète de tous les types d’équations, y compris des équations linéaires, carrées et cubiques. En élaborant une théorie systématique afin de trouver la solution des équations cubiques, il a fondé la théorie de la solution des équations algébriques.
Khayyâm a également travaillé sur la théorie mathématique de la musique en décrivant, en autres, la méthode d’extraction des degrés des entiers relatifs. Certains de ses travaux sont absolument remarquables pour leur époque. Sa définition de la physique est encore aujourd’hui un sujet d’actualité et de recherches, et une question importante de la science contemporaine. A titre d’exemple, Khayyâm avait notamment évoqué l’idée de l’existence de ce qu’on connaît aujourd’hui sous le nom de « masse noire ».

- Omar Khayyâm trouva il y a environ neuf siècles une solution géométrique à l’équation cubique en accédant à un ensemble de nombres représentant les coefficients binomiaux dans un triangle.
On utilise actuellement dans la plus grande partie du monde le calendrier grégorien, avec une erreur de vingt-six secondes dans le temps séculaire. Omar Khayyâm a conçu le sien avec une erreur de seulement douze secondes. Ce fut également lui qui annonça l’impossibilité de résoudre les équations cubiques en usant de règle et de compas, et résolut lui-même ces équations en ayant plutôt recours aux dessins géométriques basés sur les coniques.
Il a su trouver une solution générale aux équations carrées en utilisant les deux méthodes différentes d’une solution géométrique et arithmétique en même temps mais concernant les équations cubiques, il utilisa seulement les formes géométriques où il a étudié la possibilité d’existence de deux réponses à la fois. Le problème essentiel consistait dans le fait qu’à l’époque, on ne connaissait pas encore les réponses négatives et Khayyâm, par conséquence, n’y prêta aucune attention. De même, il évitait la possibilité d’obtenir trois réponses pour une équation cubique. Il réussit pourtant, quatre siècles avant Descartes, à achever l’une des plus grandes découvertes de la science en définissant le nombre comme une quantité continue, pour présenter le premier l’entier naturel et faire une démonstration selon laquelle toute quantité mathématique peut se diviser une infinité de fois. Il a également initié une conception bien ancrée en géométrie tout en recherchant un moyen pour démontrer l’axiome des parallèles ou le cinquième postulat d’Euclide.
Le triangle de Pascal
Omar Khayyâm trouva il y a environ neuf siècles une solution géométrique à l’équation cubique en accédant à un ensemble de nombres représentant les coefficients binomiaux dans un triangle, découverte attribuée à Pascal dans la tradition européenne. Pourtant, certains mathématiciens iraniens comme Al-Karaji (953-1029) ont même découvert cet ensemble bien avant Khayyâm, et en ont indiqué l’existence. Omar Khayyâm utilisa cet ensemble pour calculer le carré de la somme de deux nombres. Il trouva une démonstration pour la formule du binôme qu’il exprime dans son traité d’algèbre : « J’ai composé un livre afin d’expliquer la justesse des règles, nécessaires pour obtenir la réponse des équations cubiques et pour extraire le côté du carré, du cube, etc. Ces règles sont des nouveautés dans la science. Ces démonstrations sont arithmétiques. »
Il faut mentionner que les solutions mathématiques s’appuyaient jusqu’au XVIe siècle sur des méthodes géométriques et les mathématiciens, bien loin d’avoir accès aux symboles qui définissent une langue propice aux polémiques scientifiques, facilitant infiniment cette démarche, démontraient plutôt par un langage descriptif ordinaire. Ils résolvaient les problèmes avec des méthodes géométriques. La méthode descriptive peut être comprise de ce court fragment du traité d’algèbre de Khayyâm : « Maintenant, on présente des principes à l’aide desquels on peut trouver le nombre des monômes pour ceux dans d’autres formules du multinôme, quand un nombre se divise en deux. Comme base du travail, si tu veux ceci, mets l’« unité » sous l’« unité ». Ensuite, transmets l’ "unité" à la colonne suivante, ajoute l’« unité » qui se trouve sous la première « unité », Ce sera « deux ». Mets ce « deux » sous l’ "unité » et mets une « unité » sous le « deux ». Ce sera : « unité, deux, unité ». Cela te montre que le carré d’une somme de deux nombres est ainsi. Il faut multiplier chaque nombre en soi, car tu as aux deux côtés, l’« unité » et l’« unité » ; et tu dois multiplier deux fois un nombre à un autre, car tu as un « deux » au centre. Ainsi, tu achèveras le carré de ce nombre. Ensuite, transmets à nouveau le nombre à la colonne suivante, ajoute l’« unité » au « deux », tu achèveras « trois », écris ça sous l’« unité ». Ajoute le « deux » à l’« unité », tu achèveras le « trois ». Ecris cela sous le « trois ». Tu auras à la deuxième colonne : « unité, trois, trois, unité ». Ainsi tu pourras obtenir le cube de tout nombre, quand il a la forme de la somme de deux nombres ».
Dans son livre intitulé Discours sur les types des quarts sur la théorie de la musique, Khayyâm a procédé à une analyse mathématique de la musique, du problème de la division du quart d’une gamme à trois intervalles dans un système régulier.
Selon les renseignements disponibles à propos d’un traité perdu de Khayyâm dont le titre révèle quasiment le contenu La justesse des méthodes indiennes pour le calcul du cube et du carré, il est à dire qu’il a généralisé les méthodes indiennes pour calculer le carré et le cube d’un nombre donné. Khayyâm connaissait alors ce que l’on appelle la règle de Newton mais selon les documents historiques, les lois concernant les coefficients binômes et le triangle arithmétique – triangle de Pascal – remonterait à Karadji. Il a également résolu l’équation x3 + 200x = 20x2 + 2000 en donnant une racine positive avec l’intersection d’une hyperbole rectangulaire et un cercle. La solution numérique est trouvée approximativement par l’interpolation dans les tables trigonométriques. Il semblerait également qu’il ait conçu une théorie générale des équations cubiques dont la solution n’a pas besoin des sections coniques avec la méthode de la règle et du compas, une démarche qui sera prouvée en Europe 750 ans plus tard.

- Première page d’un manuscrit du Traité sur les preuves des problèmes en algèbre
En ce qui concerne l’algèbre [1], l’œuvre de Khayyâm dans la création du théorème géométrique des équations cubiques est le travail le plus réussi accompli par un savant iranien. Ces équations ont absorbé les mathématiciens du IXe au XVIe siècle. Les mathématiciens italiens Cardan et Tartaglia trouvèrent finalement une solution au XVIe siècle. D’autre part, Khayyâm a contribué de manière significative à la découverte de la racine positive par un argument géométrique, mais c’est seulement au XVIIe siècle que Descartes établit une relation entre la géométrie et l’algèbre. Khayyâm fut ainsi le premier à démontrer qu’une équation cubique peut avoir plus d’une seule réponse ou n’en avoir aucune.
La formule du binôme
Six cents ans avant le savant anglais Isaac Newton dont la formule porte le nom, Khayyâm est le premier a avoir présenté la formule du binôme pour les paramètres naturels dans son théorème des coefficients binominaux. Cette formule, que Newton a peut être extrait des travaux de Khayyâm, reproduite dans un langage scientifique moderne, décorée de signes et de symboles mathématiques, est ceci :
De 1074 à sa mort, Khayyâm supervisa la construction d’un grand observatoire astronomique à Ispahan, où il travailla ensuite et contribua à la réforme du calendrier solaire. En ce domaine, il fut celui qui donna la mesure de la durée de l’année de 365,24219858156 jours.
Liste des traités mathématiques d’Omar Khayyâm :
- Moshkilât al-Hisâb (Les difficultés de l’arithmétique)
- Traité algébrique sans nom.
- Risâla fi al-Barâhin al-Masâ’il al-Jabr wa al-Moqâbila (Traité sur les preuves des problèmes en algèbre)
- Sharh Moshkilât min Mosâdirât Kitâb Oqlidos (Explication sur les difficultés des définitions du livre d’Euclide)
- Jawâmi’ al-Hisâb (Encyclopédie de l’arithmétique).
- Al-Qawl ‘alâ Ajnâs al-lati bil-Arba’a (Discours sur les types des quarts)
Les travaux mathématiques de Khayyâm ont suivi trois directions : l’algèbre, la théorie des parallèles, la théorie des relations entre les entités arithmétiques ou les premières initiations avec la théorie des nombres. Dans tous ces domaines, Khayyâm eut des prédécesseurs et des successeurs importants, notamment dans les pays musulmans. Comme Aristote et Euclide, il avait commencé par l’apprentissage des œuvres classiques.
* Ville de l’est de l’Iran
Références bibliographiques :
![]() Shahriâri, Parviz, Târikh-e Riyâzidânân-e Mosâlmân (Histoire des matématiciens musulmans).
Shahriâri, Parviz, Târikh-e Riyâzidânân-e Mosâlmân (Histoire des matématiciens musulmans).
![]() Mohâseb, Gholam Hossein, Resâleh-ye Khayyâm dar bâb-e elal dar jabr (Traité de khayyâm sur les causes en algèbre, Enteshârât-e Malek, Téhéran, 1999.
Mohâseb, Gholam Hossein, Resâleh-ye Khayyâm dar bâb-e elal dar jabr (Traité de khayyâm sur les causes en algèbre, Enteshârât-e Malek, Téhéran, 1999.
![]() Arâni, Taghi, Resâleh-ye Khayyâm dar bâb-e Moshkelât-e Oqlidos (Traité de Khayyâm sur les difficultés d’Euclide), Téhéran, Enteshârât-e Jâvid, 1933.
Arâni, Taghi, Resâleh-ye Khayyâm dar bâb-e Moshkelât-e Oqlidos (Traité de Khayyâm sur les difficultés d’Euclide), Téhéran, Enteshârât-e Jâvid, 1933.
![]() Alishâhi, Ali, Sargozasht-e Riyâzidânân-e Irân va Jahân, Kholâseh yek Sokhanrâni dar Estânbul (Biographie des mathématiciens de l’Iran et du monde, extrait d’un discours à Istanbul), Revue Hebdomadaire Pouyâ, printemps 2003.
Alishâhi, Ali, Sargozasht-e Riyâzidânân-e Irân va Jahân, Kholâseh yek Sokhanrâni dar Estânbul (Biographie des mathématiciens de l’Iran et du monde, extrait d’un discours à Istanbul), Revue Hebdomadaire Pouyâ, printemps 2003.
Notes
[1] Le dictionnaire Larousse définit l’algèbre comme la science du calcul des grandeurs représentées par des lettres. En langue arabe – que les savants persans utilisaient au Moyen-âge comme le latin en Europe pour des fins scientifiques – ce mot désigne « la réunion des parties cassées".